
Contenuto
- La legge di Zipf spiegata
- Esperimento di base
- La legge di Zipf nei mercati del vapore
- Cosa possiamo imparare su Steam?
- conclusioni
Poco tempo fa un mio amico mi suggerì di guardare il video di Vsauces sulla legge di Zipf, il principio di Pareto e le loro misteriose apparizioni intorno a noi. Ecco un piccolo teaser per attirare la vostra attenzione: l'80% di tutte le persone vive nel 20% delle città più popolari; L'80% di tutti i terreni appartiene al 20% dei proprietari più ricchi; L'80% di tutta la spazzatura si trova nelle strade più pericolose del 20%, come previsto dalla legge di Zipf e dal principio di Paretos.
Non abbastanza? Bene, come ho scoperto ieri, la tana del coniglio non si ferma qui ... Pieno di scetticismo, ho deciso di guardare quanto tempo le persone trascorrono giocando ai giochi Steam ... Bene. L'80% del tempo delle persone è dedicato a giocare il 20% dei giochi più popolari ... Interessante? Bene, continuate a leggere, c'è dell'altro in questa storia.
Con un clock di oltre 20 minuti, lo sforzo di Vsauces è fantastico e spiega molte delle cose più importanti su Zipf, tuttavia è molto timido nel mostrarci il meccanismo fondamentale che è ampiamente creduto nel contribuire a spiegare perché Zipf funzioni come funziona. Quindi, prima di andare avanti, vorrei spiegarlo brevemente.
La legge di Zipf spiegata
Ci sono diversi modi concettuali per spiegare l'intuizione dietro il principio 20/80. L'esempio migliore, a mio avviso, è quello sui crateri lunari.
Esperimento di base
Quindi, immagina se vuoi, che c'è una Luna non toccata, una superficie perfettamente liscia. Ora, diciamo che ci sono alcuni asteroidi di dimensioni casuali che colpiscono la Luna, volenti o nolenti. Quando il primo asteroide atterra, lascia un cratere. Ora un altro colpisce, lasciando un cratere altrove. Ogni cratere è una parte della superficie totale, quindi c'è la possibilità che il prossimo asteroide casuale colpisca vicino a un cratere esistente e si unisca ad esso, formando un gruppo. La possibilità che un nuovo asteroide colpisca un dato cratere è quindi proporzionale alla dimensione esistente dei crateri e degli asteroidi. Ciò significa che il prossimo asteroide casuale avrà più probabilità di unirsi al gruppo più grande esistente, rendendolo ancora più grande. Una sorta di processo cumulativo, che crea quindi un meccanismo ricco di ricchezze che si fa sempre più povero.
Tenetelo a mente, perché si ritiene che questa sia la spiegazione generale del "perché" la legge di Zipfs funziona con un'universalità così misteriosa. L'esempio di asteroide è abbastanza semplice, tuttavia la domanda è cosa succederà su molte ripetizioni
Un po 'di sconcerto?
Bene, ho fatto una gif per riportare questo punto iniziale a casa. NB! il grafico sarà discusso più avanti, prova e immagina l'esperimento.

Se osserviamo la Luna reale, risulta che, man mano che la quantità di asteroidi aumenta in grandi quantità, i diametri del cratere osservati crescono in modo tale che il 20% dei crateri più grandi raggiunga l'80% di tutta la superficie.
Quindi, mentre andiamo a più asteroidi, la distribuzione dei gruppi più popolari a quelli meno popolari si avvicina a una sorta di "distribuzione ideale" con questa proprietà 20/80 - una distribuzione di Pareto. Se fai i conti, risulta che (in generale), se il gruppo più grande ha dimensione N, il secondo gruppo più grande è intorno alla taglia N / 2, il terzo N / 3 e così via e così via. Questa è chiamata la legge di Zipf. La cosa strana è la legge di Zipf e la distribuzione di Pareto opere per una quantità sconcertante di elementi (asteroidi) e gruppi (cluster di crateri). Certo, ci sono disallineamenti e disturbi casuali, ma la tendenza generale è innegabile.
Spero che tu possa vedere come gli asteroidi abbiano maggiori probabilità di colpire i grandi crateri sulla Luna e che le città siano più attraenti, se ci sono già più persone che vivono in esse. Tuttavia, bisogna rendersi conto che le città sono lontane dagli unici "gruppi" che si comportano secondo Zipf.
Ecco alcuni esempi della ricerca di Mark Newmans sulle distribuzioni di Pareto. NB! I grafici sono in scala log-log che uniformano la forma iperbolica delle curve, presentando una relazione quasi lineare.
Iniziale y = aX ^ (- b)
Log di entrambi i lati => log y = log a - b log X
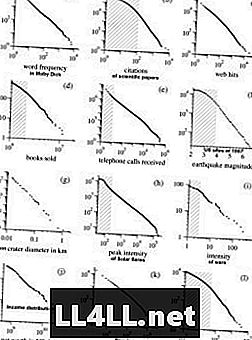
È interessante notare che la stessa tendenza viene anche dimostrata dalle sette religiose ... La proprietà condivisa della maggior parte di questi fenomeni è semplicemente questa tendenza dei "grandi gruppi che si allargano". Quindi la legge di Zipf è persistente nei meccanismi, in cui le preferenze degli elementi sono collegate positivamente alla dimensione dei gruppi (cioè, più grande è il gruppo, più è probabile che cresca). Questo è il motivo per cui mi piace pensare a gruppi come cluster e elementi come cluster.
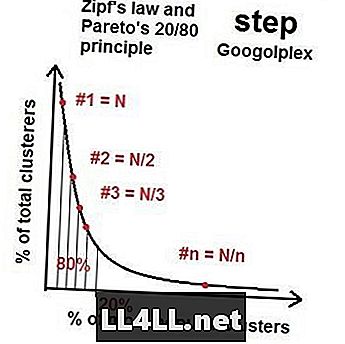
La legge di Zipf nei mercati del vapore
Sospettoso di quest'ultimo? Ecco la quantità di tempo che le persone trascorrono nei giochi più popolari su Steam .. Dati da SteamSpy.
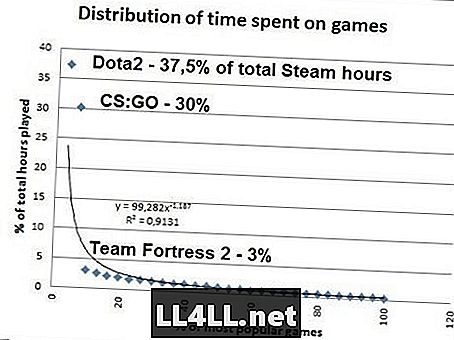
Se fai i conti, risulta che il 20% dei giochi Steam più popolari rappresenta l'80% della quantità totale di giochi, quindi il mistero Pareto 20/80 funziona come un fascino qui ... Bisogna notare, tuttavia quello per Zipf per essere vero, CS: GO deve rappresentare il 37,5% / 2 = 18,8% del tempo totale invece di un enorme 30%. Ma a parte questo outlier (STOP PLAYING CS: GO), la distribuzione simile a Zipf è chiaramente presente.
Ecco la quantità di copie vendute per i giochi più popolari.
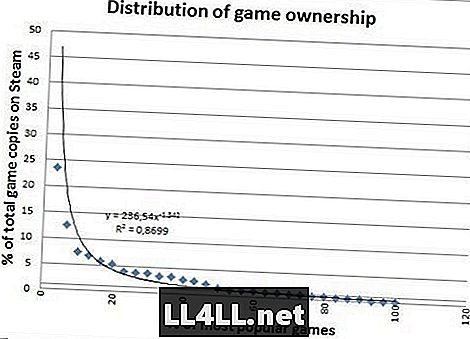
Sembra molto più bello eh? Le copie vendute non hanno grandi valori anomali, quindi si adattano molto bene, il che è una differenza degna di nota. Tuttavia, c'è qualcosa di più interessante da concludere dalle differenze degli ultimi due grafici.
Ti accorgi di come la "coda" che va a destra è una specie di grasso nel secondo grafico? Bene, in termini semplici, questo ci dice che i giochi "relativamente impopolari" sono in realtà molto più popolari che nella trama precedente.
In effetti, risulta che il 20% dei giochi più popolari rappresenta solo il 60% delle vendite, contro l'80% della riproduzione. Interessante? Scommetti che è il tuo culo.
Cosa possiamo imparare su Steam?
Bene, il fatto che la popolarità del gioco segua la distribuzione di Pareto ci dice che, in effetti, esiste un qualche tipo di effetto di rete positivo, che fa sì che i giocatori scelgano giochi che sono già giocati da più persone. Quello che la differenza di grasso delle code ci dice è che gli utenti di Steam sono molto più "group-size-blind", quando acquistano giochi rispetto a quando li giocano.
Pensaci: più le persone acquistano giochi a prescindere dall'attuale "opinione popolare", più si appiattisce la distribuzione di Pareto, poiché è meno probabile che i giochi di grandi dimensioni crescano ulteriormente. Se nessuno ha dato il culo ai topi su quante persone già giocavano e la disponibilità di tutti i giochi era la stessa, ci si aspetterebbe che il 20% dei giochi più popolari rappresentasse circa il 50% delle vendite e dei giochi (ad esempio supponendo che le preferenze individuali siano normalmente distribuito).
conclusioni
Quindi ci sono due fattori che contribuiscono alla distribuzione di Pareto nei mercati di Steam: quanto sono innovativi gli sviluppatori (quanti nuovi crateri lunari si stanno formando) e quanto i giocatori (asteroidi) valutano le dimensioni attuali del gruppo, quando si sceglie il gruppo da unire . A quanto pare, i giocatori sono molto ciechi di gruppo quando acquistano giochi, ma proprio l'opposto quando li giocano. Splendido, no?
Se vuoi saperne di più sulla legge di Zipf e sulle distribuzioni del potere, ecco una bella lezione. Inoltre, assicurati di dare un'occhiata al giornale di Newman!
Se vuoi leggere di più su questo tipo di cose, abbastanza presto cercherò di unire questa osservazione a un modello, il che dimostra che i giochi multiplayer più popolari hanno prezzi più alti (che si collegano alla preferenza dei giocatori di unirsi a gruppi di dimensioni maggiori). Vedi l'articolo qui. L'articolo di Piece De Resistance cercherà di unire queste teorie insieme spiegando come i giochi multiplayer, i social network e le città siano in realtà tutti prodotti anti-rivali con effetti di rete, (più persone consumano un bene, più vantaggi per ogni singolo consumatore) che ha li ha intitolati con questa nebbia misteriosa di Zipfian ...
Fino ad allora - divertiti!
Post scriptum Inserisci un commento con un'idea divertente per una relazione 20/80 che ritieni possa essere vera.
I miei sono:
L'80% della nostalgia delle persone è causata dal 20% dei ricordi più felici (in realtà è dimostrato dal tasso di dimenticanza delle informazioni)
L'80% della massa è concentrato nel 20% dei più grandi oggetti spaziali (effettivamente dimostrato per la distribuzione della forza gravitazionale)
E naturalmente
L'80% del disordine nel tuo bagno deriva dal 20% di ciò che mangi (nessuna ricerca accademica di cui parlare)